Rate of Change - A maths

• anpanman

  10 Apr 09, 08:28

  Water leaks out from the bottom of an inverted right circular cone of base radius  5 cm and height 15 cm into a cuboid dimensons pi cm by 9 cm, at a constant rate of 20cm3/s. Initially, the cone is filled to the brim while the cuboid container is completely empty.

  

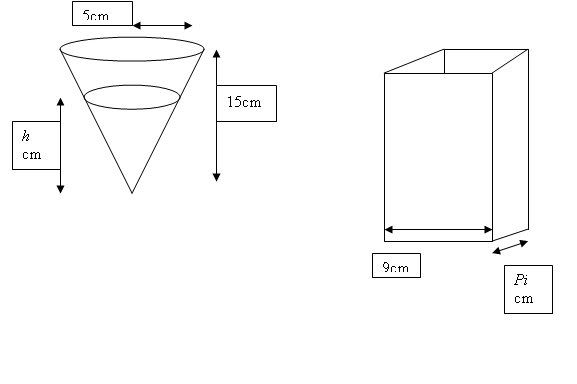
  a. Show that the volume of liquid in the cone can be expressed as V = pi*h^3 /27

  (by the way, do we find the volume initially or the volume of water within h cm as in the diagram?)

  b. Show that the uppermost  surfaces of the liquid in the cone and cuboid have the same area when the rate of decrease of height of the liquid in the cone is equal to the rate of increase of the height of the liquid in the cuboid.

  I found that the rate of decrease of water height in the cone is 180/pi*h^2 cm/s.

  Do help me out with the above questions. Been solving this since yesterday and my head's spinning over this. Lastly, thanks.

• wee_ws

  10 Apr 09, 13:19

  Hi,

    In (a), the expression that is to be shown involves the variable h yes?

    Given dV/dt = -20. We can infer that dV'/dt = 20, where V' represents the volume of liquid in the cuboid, since water leaks from cone into cuboid.

    In the case of the inverted cone, consider dh/dt = (dV/dt) (dh/dV) = -180 / (pi h^2).

    For the cuboid, volume V' = 9 pi h'. Consider dh'/dt = (dV'/dt) (dh'/dV') = 20 / (9 pi).

    Since both rates are the same in terms of magnitude,

    180 / (pi h^2) = 20 / (9 pi)

    So h = ???

    With h found, use similarity to find r (radius of the uppermost surface of the liquid in the cone).

    Then find area of this surface and compare it with 9 pi, which will be the same.

    Thanks!

  Cheers,
  Wen Shih

• anpanman

  10 Apr 09, 15:37

  Originally posted by wee_ws:

  Hi,

    In (a), the expression that is to be shown involves the variable h yes?

    Given dV/dt = -20. We can infer that dV'/dt = 20, where V' represents the volume of liquid in the cuboid, since water leaks from cone into cuboid.

    In the case of the inverted cone, consider dh/dt = (dV/dt) (dh/dV) = -180 / (pi h^2).

    For the cuboid, volume V' = 9 pi h'. Consider dh'/dt = (dV'/dt) (dh'/dV') = 20 / (9 pi).

    Since both rates are the same in terms of magnitude,

    180 / (pi h^2) = 20 / (9 pi)

    So h = ???

    With h found, use similarity to find r (radius of the uppermost surface of the liquid in the cone).

    Then find area of this surface and compare it with 9 pi, which will be the same.

    Thanks!

  Cheers,
  Wen Shih

  
  Eh, may I know the explanation to part (a)? I followed the steps given but it seems like they only lead to the solution the the second part of the question Thank you. (:

• wee_ws

  10 Apr 09, 16:35

  Hi,

    I was commenting on your question "do we find the volume initially or the volume of water within h cm as in the diagram?". Hope that clarifies.

  Cheers,
  Wen Shih

• anpanman

  12 Apr 09, 10:38

  Hi wee_ws, I still have difficulties finding the solution to part(a). It would be great if you could teach me how to do so. Thanks! (I tried differentiation and integration methods but they just don't seem to work)

   

  Edited: Found the answer. thanks anyway!