Plane Geo

• bonkysleuth

  13 Feb 09, 19:52

  In the figure ABCD and APRD are 2 circles intersecting at A and D. ARC and BPD are straight lines. Prove that PR is parallel to BC.

  I wrote about the angles in the same segment, etc.However, it still doesn't quite lead me to proving PR to be parallel to BC since the below criteria must be fulfilled in order to have 2 lines that are parallel

  They are alternate angles OR corresponding angles OR interior angles.

   

  

• d3sT1nY

  13 Feb 09, 22:06

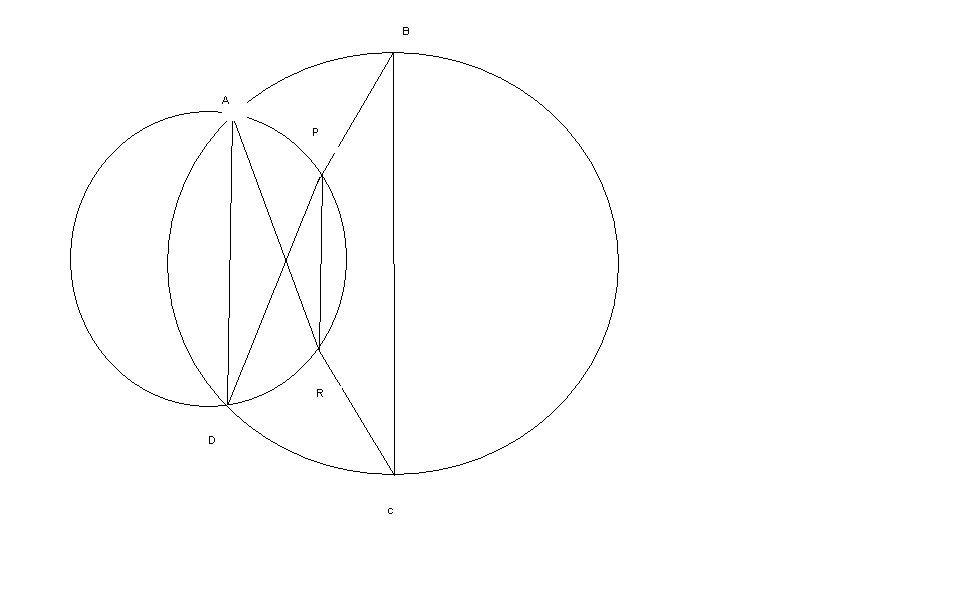
  DBC = DAC (Angles coming from the same 2 points are the same in the same circle - Big circle)

  DAR = DPR (Angles coming from the same 2 points are the same in the same circle - Small circle)

  RPB = 180 - DPR (Corresponding angles)

  RPB + DBC = 180 (Parallelogram) 

  Something like that.

  Or maybe I'm wrong. Haha.

• Mikethm

  14 Feb 09, 00:38

  Let the intersection of AC & BD be X.

  Prove that XRP and XCB are similar triangle by AAA.

  Done. (By Intercept Theorem)

• TenSaru

  14 Feb 09, 22:14

  I miss my O level maths O.o

  Anyway,

  DPR=DAR (angles in same segment)

  DAR=DBC (angles in same segment)

  Hence, DPR=DBC

  PR//BC (corresponding angle)

  1st post in this forums^^

   

• eagle

  14 Feb 09, 22:15

  Hi TenSaru

  Welcome :D