Plane Geometry

• bonkysleuth

  12 Dec 08, 19:38

  In the triangle ABC, AB = AC. D, E, and F are points on AB, BC, and CA respectively sp that DF is parallel to BC, ED is perpendicular to AB and FE is perpendicular to BC. Prove that Triangle EFD is similar to Triangle CEF. Please help. thanks! I can prove it but in an unusually tedious method which I do not know is acceptable or not. I take that the bottom part is a trapezium and gave a specific angle, say "a" and used 180 deg and all that to subtract to prove the triangles are of the same angles. Can I do so by some other method?

   

  

• Mikethm

  12 Dec 08, 23:07

  Not a different method but...

  Angle DFE = FEC = 90 degree

  Let ACB( aka FCE) = x

  ABC = x (base angle of isos triangle)

  BED

  = 180-90-x (angle sum of triangle)

  =90-x

  FED

  = 90-(90-x) (sum of angles)

  = x

  Therefore FED = ECF = x

  EDF = EFC ( angle sum of triangle)

  
  Thus Triangle EFD is similar to triangle CEF. (proven)

  
  Like dat is tedious meh?

• bonkysleuth

  13 Dec 08, 00:18

  Originally posted by Mikethm:

  Not a different method but...

  Angle DFE = FEC = 90 degree

  Let ACB( aka FCE) = x

  ABC = x (base angle of isos triangle)

  BED

  = 180-90-x (angle sum of triangle)

  =90-x

  FED

  = 90-(90-x) (sum of angles)

  = x

  Therefore FED = ECF = x

  EDF = EFC ( angle sum of triangle)

  
  Thus Triangle EFD is similar to triangle CEF. (proven)

  
  Like dat is tedious meh?

  
  But how do you know the triangle is isoceles before deriving at the solution?

• Mikethm

  13 Dec 08, 00:53

  You said that AB = AC

• anpanman

  13 Dec 08, 23:40

  Now that bonkysleuth has mentioned it. I have over here a trigo question which most of my friends and my tuition teacher have problems cracking. Anyone game to take a try?

   

  

   

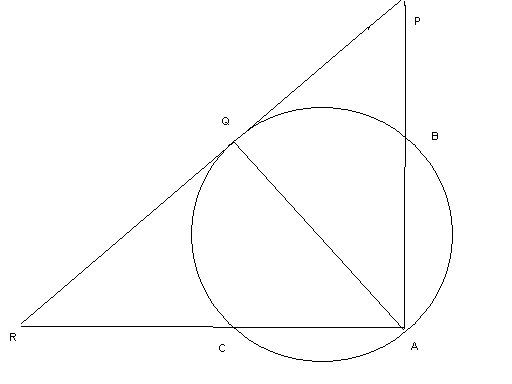
  In the diagram, A, B and C are points on the circumference of the circle and PR is a tangent to the circle at Q so that AQ is a diameter. Prove that

   

  (a) AQ^2 = AP X AB

  (b) AP X AB = AR X AC

   

  Tried using the tangent secant method. But look again. If we apply that, we have to use PQ^2 = AP X AB instead. Unless you are telling me PQ = QA so it can substitute it in the equation.

   

  An interesting question though. Hope it can be solved some day. HAHA.

• eagle

  13 Dec 08, 23:57

  Originally posted by anpanman:

  Now that bonkysleuth has mentioned it. I have over here a trigo question which most of my friends and my tuition teacher have problems cracking. Anyone game to take a try?

   

  

   

  In the diagram, A, B and C are points on the circumference of the circle and PR is a tangent to the circle at Q so that AQ is a diameter. Prove that

   

  (a) AQ^2 = AP X AB

  (b) AP X AB = AR X AC

   

  Tried using the tangent secant method. But look again. If we apply that, we have to use PQ^2 = AP X AB instead. Unless you are telling me PQ = QA so it can substitute it in the equation.

   

  An interesting question though. Hope it can be solved some day. HAHA.

  I thought it was quite simple, and in actual fact, I just looked at what is tangent secant theorem few minutes ago

  (a) PQ² = PA * PB (not AP * AB)
  But AQ² = AP² - PQ² by pythagoras theorem
  AQ² = AP² - (AP * BP)
  AQ² = AP * (AP - BP)
  AQ² = AP * AB (shown)

   

  Part b is just a repeat of part (a)
  Just need to prove that AR * AC = AQ² using the exact same method

   

  Add on: Part b is actually what intersecting secant theorem is all about.

• tut4nkh4m3n

  14 Dec 08, 00:04

  Originally posted by anpanman:

  Now that bonkysleuth has mentioned it. I have over here a trigo question which most of my friends and my tuition teacher have problems cracking. Anyone game to take a try?

   

  

   

  In the diagram, A, B and C are points on the circumference of the circle and PR is a tangent to the circle at Q so that AQ is a diameter. Prove that

   

  (a) AQ^2 = AP X AB

  (b) AP X AB = AR X AC

   

  Tried using the tangent secant method. But look again. If we apply that, we have to use PQ^2 = AP X AB instead. Unless you are telling me PQ = QA so it can substitute it in the equation.

   

  An interesting question though. Hope it can be solved some day. HAHA.

  this is siao. v limited info given man. the angle RAP might not be 90 degrees right, and then the diagram is so deceiving...

• eagle

  14 Dec 08, 00:15

  Originally posted by tut4nkh4m3n:

  this is siao. v limited info given man. the angle RAP might not be 90 degrees right, and then the diagram is so deceiving...

  You don't need RAP to be 90 degrees.

• tut4nkh4m3n

  19 Dec 08, 15:44

  lol. i totally forgot what tangent secant theorem is abt, sounds so vague. sec sch stuff? yeah. doesnt seem that hard if you know the theorem does it, ha.

• Arkansaw

  23 Dec 08, 09:25

  I dunno what is that tan-sec theorem, but ABQ and AQP are similar triangles due to AA(!)....so in fact part (a) is really simple. AQ/AP = AB/AQ

• eagle

  23 Dec 08, 22:38

  Originally posted by Arkansaw:

  I dunno what is that tan-sec theorem, but ABQ and AQP are similar triangles due to AA(!)....so in fact part (a) is really simple. AQ/AP = AB/AQ

  That's a good way also, but you have to state explicitly why the angles are equal...

  Will include in Examworld

   

  For everyone else's info, this was his solution

  Angle BAQ = angle QAP (obvious)

  Angle AQP = 90 degrees (tangent)
  Angle ABQ = 90 degrees (angle at semi circle, E maths)
  Hence, angle AQP = angle ABQ

  Thus, the triangles AQP and ABQ are similar

  Which gives us AQ/AP = AB/AQ
  And we will end up with AQ² = AP * AB (shown)

   

  A wee bit longer, but a very nice and elegant solution.

   

  In fact, by observation, we could even prove the tangent secant theorem by working backwards from here onwards through my previous solution... i.e.

  AQ² = AP * AB
  AQ² = AP * (AP - BP)
  AQ² = AP² - (AP * BP)
  But AQ² = AP² - PQ² by pythagoras theorem
  PQ² = PA * PB

  Tangent secant theorem proved(but only for the case where AQ is the diameter...)