Exponential question???

prg

10 Dec 08, 00:20

I have a few questions and doubts...

Q1 ) Show that e^x is an increasing function of x for all x. Deduce that e^x ≥1 for x ≥0

My answer:

let f(x) = e^x

f'(x) = e^x

so if x = 0,1,2,3,etc

f'(x) > 0 therefore e^x is an increasing function

for the deduce part:

let x = 0, 1, 2,etc

e^0 =1, e^1 = 2.72, e^2 =7.4, etc

therefor e^x ≥1 for x ≥0

**Have I showed and deduced this the correct way?**

Q2) By finding the area under graphs of y=e^x and y =1 between 0 and X ,where X ≥ 0, deduce that e^X ≥1+X for X ≥0 and that (e^X) ≥ 1+X +(1/2)X^2 for X ≥0

My answer :

graph:

(y=e^x)area= {0 , X} ∫ e^x dx =e^X - e^0 = e^X - 1

(y=1)area = {0 , X} ∫ 1 dx= X

from graph area: e^X - 1 ≥ X

e^X ≥ X+1

if X = 0 e^0 ≥ 1

X=1 e^1 ≥ 2

**Is this how you deduce?**

**How can we show equation: (e^X) ≥ 1+X + (1/2)X^2 for X ≥0 ? Where did + (1/2)X^2 come from??**

**How to deduce (e^X ) ≥ 1+X +(1/2)X^2 for X ≥ 0 ??**

eagle

10 Dec 08, 08:29

Q1

For the deduce part, do only for x = 0

e^0 =1

Since e^x is an increasing function as proven earlier, it follows that e^x for x≥0 will be greater or equal to e^0

Thus, e^x ≥1 (deduced)

Q2

Actually, since 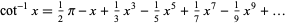, you would already know that the above is true...

Because it stated "by finding the area", we can't do that. I can't see the graph from here, but this is what I would do.

Area =
= (e^x - x) from 0 to X
= e^X -X -1

Since area ≥ 0, e^X - X - 1 ≥ 0
e^X ≥ 1 + X (deduced)

Also, because e^X ≥ 1 + X, we can expect the graph of y=e^X to be above y= 1 + X

Hence, area between y=e^X and y= 1 + X
Area2 =
= (e^x - x - ½x²) from 0 to X
= e^X -X - ½X² - 1

Since Area2 ≥ 0, e^X -X - ½X² - 1 ≥ 0
Hence, e^X ≥ 1 + X + ½X² (deduced)

Regards,
Eagle
(ExamWorld)

prg

10 Dec 08, 13:49

great, just what i needed...thanks. I see what a basic deduction requires now!!

How did u put the maths equation with the proper notation of an integral? Did u make the eq. from a software and then pasted it here?? If so then which software??

few more questions...

Q1)Find stationary value of y=lnx - x and deduce that ln x ≤ x - 1 for x >0 with equality only when x = 1.

My answer:

dy /dx = 1/x -1

if 1/x -1 = 0

x=1

stationary value : y =ln 1 -1 = -1 **Isn't this correct?**

for the deduce part:

if stationary value = -1

ln x - x (** ≤ or ≥ , how to know??**) -1

ln x ≤ x - 1

therefor if x = 1 ln 1 ≤ 0 **is this deducing correct?**

Q2) By putting x = z / y where 0< y < z, deduce Napier's inequality,

1/z < (ln z - ln y) / (z - y) < 1/y

**how to deduce this one??**

eagle

10 Dec 08, 18:51

A bit busy at the moment to take a closer look...

Mikethm, wee_ws, Ahm97sic, anyone of you around please help? I will be out till quite late tonight...

Mikethm

11 Dec 08, 01:59

Originally posted by prg:

Q1)Find stationary value of y=lnx - x and deduce that ln x ≤ x - 1 for x >0 with equality only when x = 1.

My answer:

dy /dx = 1/x -1

if 1/x -1 = 0

x=1

stationary value : y =ln 1 -1 = -1 **Isn't this correct?**

for the deduce part:

if stationary value = -1

ln x - x (** ≤ or ≥ , how to know??**) -1

ln x ≤ x - 1

therefor if x = 1 ln 1 ≤ 0 **is this deducing correct?**

You found the stationary value to be -1. With 2nd derivative, we see that

d2y/dx2 = -1/x^2

When x = 1

d2y/dx2 = -ve (max pt)

lnx -x must be equal or less than -1.

Thus lnx -x ≤ -1

ln x ≤ x-1

Qn 2 you gotta wait for someone else as I totally forgot about Napier's inequalities haha... Recommend you post it into the thread where someone is offering JC Maths help. :P

eagle

11 Dec 08, 08:35

Q2)

Actually.... I have never learnt Napier's inequality before (nor have I learned graphic calculators before).

But to me, I will treat it as a normal inequality to solve since that is what it is all about.

Divide by y throughout

===> This is what we need to prove

Graphical Method:

So what you can do is to use your graphic calculator now, and plot the follow graphs
y = x
y = 1
==> do it from values 1.05 to 20.

Then show that the graph lies under the graph y = x and above the graph y = 1 for values of x greater than 1

because z > y > 0, then z/y > 1, and thus x > 1

Analysis Method:

From Question 1, ln x ≤ x-1, and ln x = x -1 only at x = 1 (max point)
So for x>1, ln x < x -1

Hence, (x -1) / ln x < 1 (no need to change sign since both are positive)

Also, need to prove x>(x -1) / ln x
or x ln x > x - 1
or x ln x - x > -1

differentiate x ln x - x and set it to zero
ln x + 1 - 1 = 0
x = 1
At x = 1, x ln x - x = -1

second derivative, 1/x, when x = 1, gives 1 > 0
Hence, -1 is the minimum point
Thus, x ln x - x > -1 is proven
And thus x>(x -1) / ln x

Hence,

is proven.

Question and solutions will be added to ExamWorld later.

Regards,
Eagle
(ExamWorld)

prg

11 Dec 08, 23:09

few more questions!!

curve y=e^-2x -3x crosses x-axis at A (a,0) and y-axis at B(0,1)

Curve:

: