GCE A Level 2008 H2 Maths Paper 1 Question

eagle

7 Nov 08, 13:36

Originally posted by secretliker:

Note: ∫ (expression, variable, lower limit, upper limit)

5(i) Find the exact value of ∫ 1/(1+9x²), x, 0, √ 3) dx. [3]

5(ii) Find, in terms of n and e, ∫ (xⁿ ln x, x, 1, e) dx, where n ≠ -1. [4]

(i) ∫ 1/(1+9x²)dx from 0 to √3
= ∫ 1/(1+[3x]²)dx from 0 to √3
= â…“ tan^-1(3x) from 0 to √3
= â…“ tan^-1(3√3) - â…“ tan^-1(0)
= 0.46

(ii) ∫ (xⁿ ln x) from 1 to e
Integrate by parts
u = ln x, du/dx = 1/x
dv/dx = xⁿ, so v = xⁿ⁺¹ / (n+1)

∫ (xⁿ ln x) from 1 to e
= xⁿ⁺¹ / (n+1) * ln x - ∫ xⁿ / (n+1) dx from 1 to e
= xⁿ⁺¹ / (n+1) * ln x - xⁿ⁺¹ / (n+1)² from 1 to e
= [ eⁿ⁺¹ / (n+1) * ln e - eⁿ⁺¹ / (n+1)²] - [ 1ⁿ⁺¹ / (n+1) * ln 1 - 1ⁿ⁺¹ / (n+1)²]
= [eⁿ⁺¹ / (n+1) - eⁿ⁺¹ / (n+1)²]- [0 - 1 / (n+1)²]
= 1 / (n+1)² [(n+1)eⁿ⁺¹ - eⁿ⁺¹ + 1]
= 1 / (n+1)² [n*eⁿ⁺¹ + 1]

eagle

7 Nov 08, 13:53

Originally posted by secretliker:

10(i)    A student saves $10 on 1 January 2009. On the first day of each subsequent month she saves $3 more than in the previous month, so that she saves $13 on 1 February 2009, $16 on 1 March 2009, and so on. On what date will she first have saved over $2000 in total? [5]

10(ii)   A second student puts $10 on 1 January 2009 into a bank account which pays compound interest at a rate of 2% per month on the last day of each month. She puts a further $10 into the account on the first day of each subsequent month. [5]

(a)   How much compount interest has her original $10 earned at the end of 2 years? [2]

(b)   How much in total is in the account at the end of 2 years? [3]

(c)   After how many complete months will the total in the account first exceed $2000? [4]

10(i)
first term = 10
2nd term = 13
3rd term = 16
so this is an AP, first term 10, common difference 3

When sum of AP ≥ 2000
n/2 (2*10 + (n-1)*3) = 2000
n (20 + 3n - 3) = 4000
3n² + 17n - 4000 = 0
Use your graphic calculator: n=33.79 or -39.46 (reject)
So on the 34th month, she will save over $2000
Date is 1st Oct 2011

10(ii)
(a) end of 2 years = 24 months
Amount of compound interest = 10(1.02)²⁴ - 10 = $6.08

(b) end of 2nd month = 10(1.02)² + 10(1.02)
end of 3rd month = 10(1.02)³ + 10(1.02)² + 10(1.02)
end of 4th month = 10(1.02)⁴ + 10(1.02)³ + 10(1.02)² + 10(1.02)

So end of 24th month = 10(1.02)²⁴ + 10(1.02)^{23 + ... +}10(1.02)² + 10(1.02)
= sum of GP with first term 10(1.02) and common ratio 1.02 for 24 terms
= $10(1.02) (1.02²⁴ - 1) / (1.02 - 1)
= $310.3

(c) Supposed at the end of n months, the account will first exceed $2000

sum of GP with first term 10(1.02) and common ratio 1.02 for n terms ≥ 2000
10(1.02) (1.02ⁿ - 1) / (1.02 - 1) ≥ 2000
(1.02ⁿ - 1) ≥ 3.92157
1.02ⁿ ≥ 4.92157
n ≥ lg (4.92157) / lg (1.02)
n ≥ 80.475

End of 81st month, amount = 10(1.02) (1.02⁸¹ - 1) / (1.02 - 1) = $2026.20
Start of 81st month = $2026.2 / 1.02 = $1986.47 (not needed, show for fun only)

The account first exceed $2000 after 81 complete months.

secretliker

7 Nov 08, 15:18

Oops, so sorry, 5(i) should be integrating 0 to 1/√3

f'(x) = sec² (2x + ¼π) * 2 = 2 sec² (2x + ¼π)
f''(x) = 4 sec (2x + ¼π) * sec (2x + ¼π) tan (2x + ¼π) *2
= 8 sec² (2x + ¼π) tan (2x + ¼π)

Need to also differentiate the expression inside?

AC = (4 + 3θ^²)^0.5
Hence, a = 4, b = 3

Haven't yet.

secretliker

7 Nov 08, 15:20

When sum of AP ≥ 2000
n/2 (2*10 + (n-1)*3) = 2000
n (20 + 3n - 3) = 4000
3n² - 17n - 4000 = 0

Should be plus.

eagle

7 Nov 08, 15:20

Originally posted by secretliker:

Oops, so sorry, 5(i) should be integrating 0 to 1/√3

Need to also differentiate the expression inside?

Haven't yet.

Already done... I skipped it and changed the first number from 2 to 4

The triangle question, isn't it already proved? What you mean by haven't yet?

eagle

7 Nov 08, 15:23

Originally posted by secretliker:

Should be plus.

changed :D

always so prone to careless when I typed it out immediately :(

secretliker

7 Nov 08, 15:25

a and b not 4 and 3, cos still need to expand out.

AC ≈ (4 + 3θ²)^½ ≈ a + bθ²

eagle

7 Nov 08, 15:36

Originally posted by secretliker:

a and b not 4 and 3, cos still need to expand out.

AC ≈ (4 + 3θ²)^½ ≈ a + bθ²

oh ya, see wrongly

Sub θ = 0, see that a = 2
Sub θ = 0.1,
LHS = 2.0075
RHS = 2 + 0.01b
so b = 0.75

So a = 2, b = 0.75

Can do Maclaurin's expansion as well to prove, but I'm lazy to do so.

To check,
Sub θ = 0.2
LHS = 2.029778
RHS = 2.03
Very close, so highly likely to be correct

X1ao-lang

7 Nov 08, 16:36

hello! question 10. 34 months. i got that. but shouldnt it be Oct 2011.

Jan2009 to Jan 2010 12 months

Jan 2010 to Jan 2011 another 12 months.

then Jan 2011 to Oct 2011 10 months.

total: 34months. did i count wrongly?

eagle

7 Nov 08, 16:37

u r right, my mistake

JialatZz

7 Nov 08, 19:45

Oh no ... for e compound interest i got like 82 months !!!!!!!!!!!! DIEEEEEEEEEEEEEE

secretliker

7 Nov 08, 19:54

f'(x) = sec² (2x + ¼π) * 2 = 2 sec² (2x + ¼π)
f''(x) = 4 sec (2x + ¼π) * sec (2x + ¼π) tan (2x + ¼π)
= 4 sec² (2x + ¼π) tan (2x + ¼π)

Originally posted by eagle:

Already done... I skipped it and changed the first number from 2 to 4

Differentiate 2 sec² (2x + ¼π).
= 2(2) sec (2x + ¼π) * d/dx [sec (2x + ¼π)]
= 4 sec (2x + ¼π) * sec (2x + ¼π) tan (2x + ¼π) * d/dx (2x + ¼π)
= 4 sec (2x + ¼π) * sec (2x + ¼π) tan (2x + ¼π) * 2
= 8 sec (2x + ¼π) * sec (2x + ¼π) tan (2x + ¼π)

I was referring to the bold part. So the final coefficient should be 8?

jaydunkfull

7 Nov 08, 20:20

how do you type pi? cant find the symbol.

change e world

8 Nov 08, 21:30

Originally posted by eagle:

6(a) Draw triangle out
Use cosine rule

AC^{² = AB²} ^{+ BC²} ^{- 2(AB)(BC)cos} θ
AC² = 1 + 9 - 2(1)(3)(1 - θ^²/2) since θ is small
AC² = 10 - 6 + 6θ^²/2
AC = (4 + 3θ^²)^0.5

Sub θ = 0, see that a = 2
Sub θ = 0.1,
LHS = 2.0075
RHS = 2 + 0.01b
so b = 0.75

So a = 2, b = 0.75

Can do Maclaurin's expansion as well to prove, but I'm lazy to do so.

To check,
Sub θ = 0.2
LHS = 2.029778
RHS = 2.03
Very close, so highly likely to be correct

6(b) Long time since I did Maclaurin's Series.
f(x) = tan (2x + ¼π)

f'(x) = sec² (2x + ¼π) * 2 = 2 sec² (2x + ¼π)
f''(x) = 4 sec (2x + ¼π) * sec (2x + ¼π) tan (2x + ¼π)
= 4 sec² (2x + ¼π) tan (2x + ¼π)

f(0) = tan (¼π) = 1
f'(0) = 2 sec² (¼π) = 4
f''(0) = 4sec² (¼π) tan (¼π) =8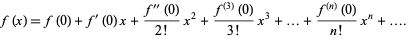

Thus,
first term = 1
second term = 4
third term = 8/2! = 4

actually f'(x) = 2sec^2 (2x + 1/4 pi)

= 2 + 2tan^2 (2x + 1/4 pi)

= 2 + 2 [f(x)]^2

so f''(x) = 4 [f(x)][f'(x)] is it?..

secretliker

8 Nov 08, 22:14

Originally posted by change e world:

actually f'(x) = 2sec^2 (2x + 1/4 pi)

                     = 2 + 2tan^2 (2x + 1/4 pi)

                     = 2 + 2 [f(x)]^2

so f''(x) = 4 [f(x)][f'(x)] is it?..

Yes.

f''(x) = 4 [f(x)][f'(x)]

= 4 [ tan (2x + ¼π) ] [ 2 sec^2(2x + 1/4 pi) ]

= 8 ...

Final coefficient should be 8.