GCE A Level 2008 H2 Maths Paper 1 Question
-

I got the answers as x = 6.09, y = 12.6. Dunno if correct.
-
Form equation
9 * π x/2 + 3 * (x + 2y) = 180
3π x/2 + x + 2y = 60
y = 30 - 3π x/4 - x/2Total area
= xy + πx²/8
= x (30 - 3π x/4 - x/2) + πx²/8
= 30x - 3π x²/4 - x²/2 + πx²/8dA/dx = 30 - 3π x/2 - x + πx/4
when dA/dx = 0,
30 + (π/4 - 3π/2 - 1)x = 0
(π/4 - 3π/2 - 1)x = -30
x = 6.09 my = 30 - 3π x/4 - x/2
y = 12.6 m -
Thanks, how is it possible this is worth 10 marks?
-
where u get this question from?
Sometimes the marking scheme very funny... Last time I did this Maths S paper mechanics question, solved it in 3 lines using conservation of energy; it was worth 7 marks
-
This is 2008 H2 Maths P1.
I think marker was expecting people to use the method from the marking scheme. So did you get 7 marks for 3 lines?
-
Originally posted by secretliker:

I got the answers as x = 6.09, y = 12.6. Dunno if correct.
good for you, u got the correct ans + 10 marks. -
Originally posted by secretliker:
This is 2008 H2 Maths P1.
I think marker was expecting people to use the method from the marking scheme. So did you get 7 marks for 3 lines?
that was a past year question. I showed to my teacher my method, and he said it was ok.
The required method was to use integration to solve for part (i) and (ii) (each 7 marks), and the method was similar for both parts. However, for (ii), I could make use of my physics knowledge to solve it with part (i)'s answer, that's why.
Any more 2008 Maths questions to confirm answers?
-
I remember my O Level got a P&C question worth 6 marks which I only took 1 line to solve.
Yeah, still got more questions.
8. A graphic calculator is not to be used in answering this question.
(i) It is given that z1 = 1 + (√3)i. Find the value of z13, showing clearly how you obtain your answer. [3]
(ii) Given that 1 + (√3)i is a root of the equation
2z3 + az2 + bz + 4 = 0,
find the values of the real numbers a and b. [4]
(iii) For these values of a and b, solve the equation in part (ii), and show all the roots on an Argand diagram. [4]
-
11. The equations of three planes, p1, p2, p3 are
2x – 5y + 3z = 3,
3x + 2y – 5z = -5,
5x + λy + 17z = μ,
respectively, where λ and μ are constants. When λ = -20.9 and μ =16.6, find the coordinates of the point at which these planes meet. [2]
The planes p1 and p2 intersect in a line l.
(i) Find a vector equation of l. [4]
(ii) Given that all three planes meet in the line l, find λ and μ. [3]
(iii) Given instead that the three planes have no point in common, what can be said about the values of λ and μ? [2]
(iv) Find the Cartesian equation of the plane which contains l and the point (1, -1, 3). [4]
-
Originally posted by secretliker:
I remember my O Level got a P&C question worth 6 marks which I only took 1 line to solve.
Yeah, still got more questions.
8. A graphic calculator is not to be used in answering this question.
(i) It is given that z1 = 1 + (√3)i. Find the value of z13, showing clearly how you obtain your answer. [3]
(ii) Given that 1 + (√3)i is a root of the equation
2z3 + az2 + bz + 4 = 0,
find the values of the real numbers a and b. [4]
(iii) For these values of a and b, solve the equation in part (ii), and show all the roots on an Argand diagram. [4]
damn... I forgot a lot of my once strong complex numbers :(
But these look simple enough, shall try
(i) (1 + (√3)i)3 = 13 + 3(1)² ((√3)i) + 3(1)((√3)i)² + ((√3)i)3
= 1 + 3(√3)i - 9 - 3(√3)i
= -8(ii) (1 + (√3)i)² = 1² + 2 (√3)i + 3i²
= -2 + 2 (√3)i2z3 + az2 + bz + 4 = 0
Sub z = 1 + (√3)i2(-8) + a(-2 + 2 (√3)i) + b(1 + (√3)i) + 4 = 0
(-16 -2a +b + 4) + (2a(√3) + b(√3))i = 0
Hence,
-16 -2a +b + 4 = 0 ====> -2a + b = 12 ---------------(1)
2a(√3) + b(√3) = 0 ====> 2a + b = 0 -----------------(2)(1) + (2): 2b = 12
b = 62a + b = 0
a = -3(iii) Thus, the equation is
2z3 - 3z2 + 6z + 4 = 0
Roots are 1 + (√3)i (given) and 1 - (√3)i (complimentary)
Also, sub z = -0.5 ====> (not sure can play cheat like that a not, if cannot hv to use long division)
2(-0.5)3 - 3(-0.5)2 + 6(-0.5) + 4 = -0.25 - 0.75 - 3 + 4 = 0
Hence, z = -0.5 is also a rootThus, z = 1 + (√3)i, 1 - (√3)i, -0.5
Argand diagram should be easy to draw
-
Originally posted by secretliker:
11. The equations of three planes, p1, p2, p3 are
2x – 5y + 3z = 3,
3x + 2y – 5z = -5,
5x + λy + 17z = μ,
respectively, where λ and μ are constants. When λ = -20.9 and μ =16.6, find the coordinates of the point at which these planes meet. [2]
The planes p1 and p2 intersect in a line l.
(i) Find a vector equation of l. [4]
(ii) Given that all three planes meet in the line l, find λ and μ. [3]
(iii) Given instead that the three planes have no point in common, what can be said about the values of λ and μ? [2]
(iv) Find the Cartesian equation of the plane which contains l and the point (1, -1, 3). [4]
Damn... I also forgot a lot of vectors... Last time I also damn power one :(
Also shall try with what I rememberI think you can use graphic calculator to solve... I use my calculator (not graphic) to solve for 3 unknowns
x = -0.367, y=-0.367, z = 0.636(i) 2x – 5y + 3z = 3 ---- (1)
3x + 2y – 5z = -5 ---- (2)line parallel to both planes = (2, -5, 3) x (3, 2, -5)
= (19,19,19) = 19 (1,1,1)Add (1) and (2) gives
5x - 3y - 2z = -2
Let x = 0, y = 0, so z = -1
(0,0,-1) is a point on both planesso, equation of vector l = (0,0,-1) + t (1,1,1)
(ii) (5,λ,17) dot (1,1,1) = 0
5 + λ + 17 = 0
λ = -225x + -22y + 17z = μ
Sub (0,0,-1)
μ = -17(iii) Three planes have no points in common, means p3 does not intersect vector l
Means p3 must be parallel to vector l, but have no points on vector l
Thus, λ will still be -22, and μ can be anything except -1
(iv) Plane must also contain (0,0,-1)
Contain (1,-1,3)
and be perpendicular to (1,1,1)Vector between (0,0,-1) and (1,-1,3) is (1,-1,4)
So plane must be perpendicular to both (1,1,1) and (1,-1,4)
Use cross product
(1,1,1) x (1,-1,4) = (5,-3,-2)
so cartesian equation of plane is 5x -3y -2z = D
sub in (0,0,-1)
D = 2
So final answer: 5x -3y -2z = 2 -
so in your opinion, was this yr's math significantly harder? or is it avg/ easy?
-
so far these 3 questions looked simple enough... although I forgot a bit of vectors and hv to spend a little time revising and confirming what I remembered just now...
-
simple? for you, or by A level standards?
-
at least to me, by A level standards
cuz I dun specialise in maths, and I have been rather out of practice (and forgot quite a bit), only occasionally giving tuition to my sis. And I know if I was back to my own peak in my 2001 A levels, these are seriously very very standard questions.
and if I can do it, I believe there are many many others out there who could do it as well.
But it's hard to judge a whole paper only from these 3 questions.
Anyway, don't bother with what I said. Afterall, I was from the C maths F maths stream, so maths was something like my livelihood. Just go practice hard and score for paper 2. If you need help in any of the topics, I will source and search and put up some questions on ExamWorld
-
den i'm quite screwed...
-
depends on what you are aiming to do after As.
If you want to go into arts in uni, then the requirements aren't that high
Unless you want to go into medicine, law or take up some scholarship, then u need the A
A levels is just a stepping stone upwards
-
its more of a aim thingy.
i want to get at least 3 H2 As.
in other words, the more As the merrier.
-
I think statistics show that to be safe that you will go into uni, need at least 69 out of 90 rank points.
Eagle your solutions really quite short and sweet. My solutions a whole lot longer.
Anyway, for Qn 11, the first part the answer can be (-4/11, -4/11, 7/11)?
Although my calculator can't express it in fraction when I press the button, but I know the value -0.363636.. is -4/11, so can write as -4/11?
I'll go type more questions and then post up. The other questions should be even easier.
-
6(a) In the triangle ABC, AB = 1, BC = 3 and angle ABC = θ radians. Given that θ is a sufficiently small angle, show that
AC ≈ (4 + 3θ2)½ ≈ a + bθ2,
for constants a and b to be determined. [5]
6(b) Given that f(x) = tan (2x + ¼π), find f(0), f’(0) and f’’(0). Hence find the first 3 terms in the Maclaurin series of f(x). [3]
-
5(i) Find the exact value of ∫ 1/(1+9x2), x, 0, 1/√ 3) dx. [3]
5(ii) Find, in terms of n and e, ∫ (xn ln x, x, 1, e) dx, where n ≠ -1. [4]
10(i) A student saves $10 on 1 January 2009. On the first day of each subsequent month she saves $3 more than in the previous month, so that she saves $13 on 1 February 2009, $16 on 1 March 2009, and so on. On what date will she first have saved over $2000 in total? [5]
10(ii) A second student puts $10 on 1 January 2009 into a bank account which pays compound interest at a rate of 2% per month on the last day of each month. She puts a further $10 into the account on the first day of each subsequent month. [5]
(a) How much compount interest has her original $10 earned at the end of 2 years? [2]
(b) How much in total is in the account at the end of 2 years? [3]
(c) After how many complete months will the total in the account first exceed $2000? [4]
Note: ∫ (expression, variable, lower limit, upper limit)
-
yay i love you! i got the garden qns correct! i didnt know how to do the complex numbers one. and for the triangle questions, i got stuck at 4+3@ part, didnt know how to convert to that required form. and i didnt know how to do the vectors qns. :( tell me how screwed i am
-
10 c, my answer was 34months, 1 october 2011
-
Originally posted by secretliker:
I think statistics show that to be safe that you will go into uni, need at least 69 out of 90 rank points.
Eagle your solutions really quite short and sweet. My solutions a whole lot longer.
Anyway, for Qn 11, the first part the answer can be (-4/11, -4/11, 7/11)?
Although my calculator can't express it in fraction when I press the button, but I know the value -0.363636.. is -4/11, so can write as -4/11?
I'll go type more questions and then post up. The other questions should be even easier.
ya, in fractions also can
The rest of the questions I do tmr... A bit tired...
-
Originally posted by secretliker:
6(a) In the triangle ABC, AB = 1, BC = 3 and angle ABC = θ radians. Given that θ is a sufficiently small angle, show that
AC ≈ (4 + 3θ2)½ ≈ a + bθ2,
for constants a and b to be determined. [5]
6(b) Given that f(x) = tan (2x + ¼π), find f(0), f’(0) and f’’(0). Hence find the first 3 terms in the Maclaurin series of f(x). [3]
6(a) Draw triangle out
Use cosine ruleAC² = AB² + BC² - 2(AB)(BC)cos θ
AC² = 1 + 9 - 2(1)(3)(1 - θ²/2) since θ is small
AC² = 10 - 6 + 6θ²/2
AC = (4 + 3θ²)^0.5Sub θ = 0, see that a = 2
Sub θ = 0.1,
LHS = 2.0075
RHS = 2 + 0.01b
so b = 0.75
So a = 2, b = 0.75Can do Maclaurin's expansion as well to prove, but I'm lazy to do so.
To check,
Sub θ = 0.2
LHS = 2.029778
RHS = 2.03
Very close, so highly likely to be correct6(b) Long time since I did Maclaurin's Series.
f(x) = tan (2x + ¼π)
f'(x) = sec² (2x + ¼π) * 2 = 2 sec² (2x + ¼π)
f''(x) = 4 sec (2x + ¼π) * sec (2x + ¼π) tan (2x + ¼π)
= 4 sec² (2x + ¼π) tan (2x + ¼π)f(0) = tan (¼π) = 1
f'(0) = 2 sec² (¼π) = 4
f''(0) = 4sec² (¼π) tan (¼π) =8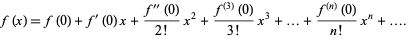
Thus,
first term = 1
second term = 4
third term = 8/2! = 4