[E-Maths] Compound Interest
-
Right now I'm doing revision onthe topic of financial transactions, and compound interest is particularly stumping me.
Just as an example, here's a question regarding compound interest:
Carol deposits $800 in a bank that offers interest of 3% per annum. If the money and its interest rate are not withdrawn but allowed to compound annually, how much will she have at the end of three years? (Give your answer correct to the nearest cent.)
I got 1036.02; the answer was 874.18. What am I doing wrong here?
-
take 800 * 1.03³ = 874.18
Perhaps you should show your workings here, then we can explain to you what went wrong.
-
You never show working.
How is anyone going to know where you went wrong?
874.18 is correct.
-
What I did was:
800 (1 + (3% x 3))^3 (3% was calculated as 3/100)
800 (1 + (9/100)^3
800 X 1.295029
...which eventually comes out to 1036.0232 or 1036.02 when rounded to the nearest cent.
I did everything on a calculator, so there's little chance of things going wrong. Still, I have edited my full workings into the post.
I still don't get the formula; what am I doing wrong?
-
Originally posted by maurizio13:
You never show working.
How is anyone going to know where you went wrong?
874.18 is correct.
Working shown above; apologies for ommiting that.
-
Originally posted by eX.A.K.R.:
What I did was:
800 (1 + (3% x 3))^3 (3% was calculated as 3/100)
...which eventually comes out to 1036.0232 or 1036.02 when rounded to the nearest cent.
I still don't get the formula; what am I doing wrong?
800 (1 + (3% x 3))^3The ones in red are not needed.
-
I see... so I do not need to multiply the interest rate by the number of times it is compounded along with raising the thing to the number of times it was compounded, but only needed to do the latter... am I right?
Thanks for that, and I will keep this thread under my eye just in case I need it again.
-
Originally posted by eX.A.K.R.:
I see... so I do not need to multiply the interest rate by the number of times it is compounded along with raising the thing to the number of times it was compounded, but only needed to do the latter... am I right?
Thanks for that, and I will keep this thread under my eye just in case I need it again.
Compound Interest:
Principal x (1 + r)^n
r = interest rate
n = year
You got your simple interest and compound interest mixed up, so you ended up combining both.
Simple Interest:
Principal x (1 + n(r))
r = interest rate
n = year (ie if your interest rates is per year)
-
Compoud interest formula is not taught at O Level. Under SEAB E math syllabus, students are required to calculate compoud interest without the use of formula.

At the end of year 1:
$800 x 103% = $824
At the end of year2:
$824 x 103% = $848.72At the end of year 3:
$848.72 x 103% = $874.1816 = $874.18 (nearest cent) -
Originally posted by Darkness_hacker99:
Compoud interest formula is not taught at O Level. Under SEAB E math syllabus, students are required to calculate compoud interest without the use of formula.

At the end of year 1:
$800 x 103% = $824
At the end of year2:
$824 x 103% = $848.72At the end of year 3:
$848.72 x 103% = $874.1816 = $874.18 (nearest cent)His calculation already has formula.

Wonder who taught him?
He combined the 2 formula to make a mega formula.
-
actually it is not really a formula... ;)
-
Originally posted by maurizio13:
His calculation already has formula.

Wonder who taught him?
He combined the 2 formula to make a mega formula.
Hi Maurizio13,
This is a question posted in another forum.
Question
If a person invests $1000 every year at an interest rate, r, 20 years later the person will have $150,000.
This person uses geometric progression to work out the interest rate r and the person works until
150000 - 150000r = 1000r = 1000r^20
What will be the interest rate, r ?
The question is probably posted by a finance student and the question probably does not allow the use of a financial calculator to work out the interest rate r. Otherwise the student can simply use a financial calculator to work out the interest rate r.
Regards,
ahm97sic
-
Originally posted by Ahm97sic:
Hi Maurizio13,
This is a question posted in another forum.
Question
If a person invests $1000 every year at an interest rate, r, 20 years later the person will have $150,000.
This person uses geometric progression to work out the interest rate r and the person works until
150000 - 150000r = 1000r = 1000r^20
What will be the interest rate, r ?
The question is probably posted by a finance student and the question probably does not allow the use of a financial calculator to work out the interest rate r. Otherwise the student can simply use a financial calculator to work out the interest rate r.
Regards,
ahm97sic
oh ya, CNA forums :D
I can only use estimation to solve it :( And still a little inaccurate
-
Entry is deleted.
-
My answer :D
Actually can get a very very very rough estimate (sry... engineers work with rough estimates)
Assume r is insignificant from r^5 onwards
(1+r)^20 -151r -1 = 0
1 + 20r + 190r^2 + 1140r^3 + 4845r^4 -151r - 1 = 0
r (4845r^3 + 1140r^2 + 190r - 131) = 0
solving, r = 0 (reject), -0.22 (reject) or 0.21
So roughly 21%, 3% difference from the 18.17%
and to me, 0.21^5 = 0.0004 is very very small -
I must protest that this question is not Finance, it's more Actuarial than Finance. Did Actuarial about 7 years ago, but forgotten most of it.
1000 (1-(1 + i)^20) / (1-(1+i)) = 150,000
Solve for i.
I am not good with mathematical manipulations, but I put it to my graphic calculator.
i = 0.1818884124
I am sure eagle can manipulate the equation best.

N.B. This is an accumulated value of an annuity due, that means first payment is at year 0 and not year 1.
-
Sum of Geometric Sequence:
S = a ((1-r^n)/(1-r))
The (1+i) is the r term in the Geometric Sequence.
-
if it is to 1 s.f., my estimation is accurate

-
compound interest formulae is given. at least that's what i saw in the n level emaths TYS. any changes recently?
-
This is hardly simple or compound interest, pity the O level students.
-
Ok.
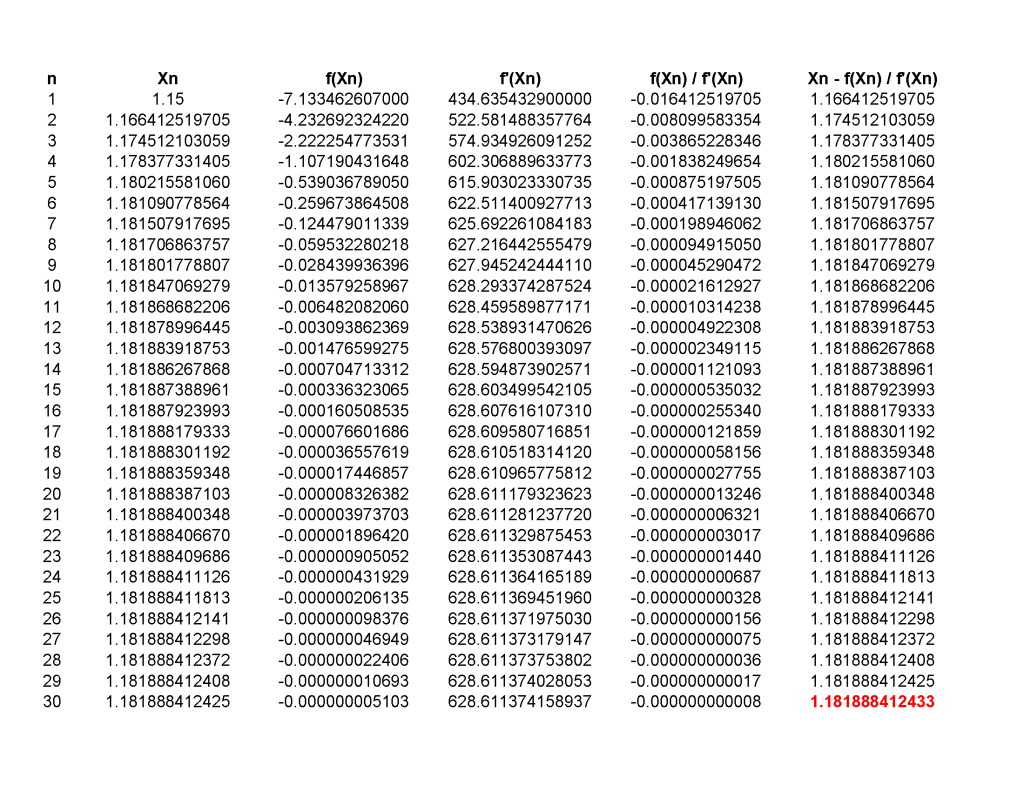
If don't use calculator can use Newton-Raphson Method to approximate, after 20 iterations it's almost as accurate as my calculator.
Of course I used spreadsheet lah, only took few minutes, you can slowly use paper to calculate everything.

-
Arghhh Actuarial Mathematics and LT Stats...this module effectively has the record of leaving me sleepless for 6 nights


-
Hmmm.......
Come to think of it, might be able to do linear interpolation or bisection method also.
-
Linear Interpolation:
15%:
1,000 (1-(1+0.15)^20) / (1-(1+0.15)) = 102,443.58
20%:
1,000 (1-(1+0.20)^20) / (1-(1+0.20)) = 186,688.00
(i - 0.15) / (0.20 - 0.15) = (150,000.00 - 102,443.58) / (186,688.00 - 102,443.58)
i = 0.178225264
It's a rough approximation because the two interest rates are too far apart from the actual value (15% and 20%). If it's closer, the values would be more accurate.
-
Linear Interpolation:
18%:
1,000 (1-(1+0.18)^20) / (1-(1+0.18)) = 146,627.97
18.3%:
1,000 (1-(1+0.183)^20) / (1-(1+0.183)) = 152,022.19
(i - 0.18) / (0.183 - 0.18) = (150,000 - 146,627.97) / (152,022.19 - 146,627.97)
i = 0.181875357