Integration Question

• Ahm97sic

  12 Oct 08, 22:57

  For new 2008 add maths syllabus students

  This question combines the modulus function with integration.

  Perhaps you will like to solve it.

  Question  

  Integrate l x^2 + 2x -3 l dx from x = 0 to x = 2

  [The sign in blue is the modulus sign]

  Thank you for your kind attention.

  Regards,

  ahm97sic

• iamapebble

  12 Oct 08, 23:03

  I don't know what to do with the modulus function ):

  I only know that if I integrate x^2 + 2x -3 dx I will get (if there's no careless mistake)      x^3/3 + x^2 - 3x + c

  >< Care to enlighten?

• Garrick_3658

  12 Oct 08, 23:10

  I think I would do this:

  x^2 + 2x - 3 = (x-1)(x+3)

  Square it, and the modulus is gone.

  so integrate (x-1)^2(x+3)^2

  integrate x^4+4x^3-2x^2-12x+9

  = x^5/5 + x^4 - 2/3x^3 - 6x^2 + 9x + c

  Any mistakes/misconceptions?

  Hopefully this doesn't come out in the exam.

  EDIT: I made a mistake, can't pinpoint, but I cannot just square an equation without warning. I shall wait for some directions for corrections

• davidche

  12 Oct 08, 23:46

  How can you just square it? I think the direction to square it is correct. But, i would do this:

  Square root (integrate square of the function)

  or integrate (square root(square of the function))

  kinda literal dont you think? XD

• eagle

  12 Oct 08, 23:50

  pple... dun do till so troublesome...

  first, you must note which part is positive and which is negative... A simple method is to do a quick sketch of the graph.

  For e.g., x² + 2x - 3 = (x-1)(x+3)
  The roots are -3 and 1, and since it is a U shaped curve, anything where x is such that -3 < x < 1 is smaller than zero

  For integrating from x = 2 to x =0, it is the same as the negative of integrating from x = 0 to x = 2

  Note that for x between 0 and 1, x² + 2x - 3 is negative
  for x between 1 and 2, x² + 2x - 3 is positive

  So,

  integrate |x² + 2x - 3| from x = 2 to x = 0
  = - integrate |x² + 2x - 3| from x =0 to x = 2
  = - [integrate -(x² + 2x - 3) from x = 0 to x = 1 + integrate x² + 2x - 3 from x =1 to x = 2]
  ============> add a negative sign for 0<x<1 because the mod sign flipped it from negative to positive; a minus sign does the same thing for the negative portion

  = - [ (-x³/3 - x² + 3x) from x = 0 to x =1  +  x³/3 + x² - 3x from x = 1 to x = 2]
  = - [ (1.667 - 0 ) + (0.667 - (-1.667))]
  = -4

   

  Regards,
  Eagle
  (ExamWorld)

   

  Edit: Just realised it was Ahm97sic who posted out the question for everyone :D
  But nvm... Already answered... Good question though :D

• Garrick_3658

  13 Oct 08, 00:41

  So, it's like you're totally ignoring the modulus sign? Since modulus reflected the graph to positive shouldn't your area be positive too?

• eagle

  13 Oct 08, 00:49

  Originally posted by Garrick_3658:

  So, it's like you're totally ignoring the modulus sign? Since modulus reflected the graph to positive shouldn't your area be positive too?

  that's because the integration is from 2 to 0, not 0 to 2

   

• Garrick_3658

  13 Oct 08, 01:04

  Mind doing some further explanations between integration and modulus? I still don't get it.

• Ahm97sic

  13 Oct 08, 01:16

  Hi Garrick_3658, iamapebble and Davidche

  Question  

  Integrate l x^2 + 2x -3 l dx from x = 0 to x = 2

  [The sign in blue is the modulus sign]

  Answer

  Step 1 : Sketch the curve y = x^2 + 2x -3

  The curve will be an "U-shaped" curve.

  The curve will cut the x-axis at x = 1 and x = - 3

  Part of the curve will be below the x-axis.

  Step 2 : Sketch the curve y =   l x^2 + 2x - 3 l

  Part of the curve that is previously below the x-axis will be reflected to be above the x-axis.

  It will be observed that the area from x = 1 to x = 2 is positive.

  The area from x = 0 to x = 1 will be positive too but it will be difficult to integrate to find this area using the modulus function, so instead we will integrate the curve  y = x^2 + 2x - 3 that is below the x-axis from x = 0 to x = 1. These two areas are the same as these areas are the reflection of one another.

  Step 3 : Find the area

   Integrate l x^2 + 2x -3 l dx from x = 0 to x = 2

   = Integrate  x^2 + 2x -3 dx from x = 1 to x = 2

      + Integrate [- ( x^2 + 2x -3)] dx from x = 0 to x = 1

  = 4

  So, you have learnt the trick of solving this type of question. So, now you know how to solve it if this type of question comes out in the "O" level add maths exam.

  Thank you for your kind attention.

  Regards,

  ahm97sic

• eagle

  13 Oct 08, 01:19

  ahm97sic, from your answer, I think you should phrase it as integrating from x = 0 to x = 2

  Not the other way round :D

• Ahm97sic

  13 Oct 08, 01:23

  Entry is deleted.

• eagle

  13 Oct 08, 01:29

  hi ahm97sic

   

  the terminology is incorrect

  means a and b are the lower limit and upper limit of the integration

  It means integrating from x = a to x = b

  This is because

  

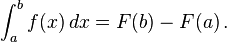
  Going the other way round, you will have to put a negative sign.

  Integrating from x = 2 to x = 0 is equal to the negative of integrating from x = 0 to x = 2

  
  

  
  

   

• Ahm97sic

  13 Oct 08, 01:36

  Hi Eagle,

  Yes, the terminology that I used in the question is incorrect.

  It should be to integrate from x = 0 to x = 2.

  I will make the changes to the question now.

  Regards.

  ahm97sic.

• iamapebble

  13 Oct 08, 10:08

  Ohhhh I just saw the question requres x = 0 to x = 2, no wonder I was thinking why everyone do so long steps, hehe. Anyway, thanks! I get it now! :D

• FirePig

  13 Oct 08, 11:11

  eagle has sharp eyes.

• Lee012lee

  13 Oct 08, 12:15

  Eagle don't wear spectacles ok.

• jinjia

  15 Oct 08, 00:30

  ohh i'm worried about my amaths alr.. i dont seems to be able to make it for this type of questions in Os.