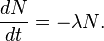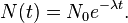Help in A level physics questions (nuclear physics.)

• lavastar

  1 Jun 08, 00:21

  1)The radioactive isotope 232,92U (meaning mass number =232, proton number = 92) emits alpha particles with an energy of 5.30MeV and has a half life of 74years. For a sample containing 1.30 X 10^24 atoms, calculate the maximum theoretical power output. ( ans : 3300W)
  
  2)A patient is to be given an injection of iodine-131 in investigation of her blood volume.Sample A is injected into the patient while sample B is set on one side.
  Each sample has an initial activity of 8000 Bq and iodine-131 has halflife of 8 days.
  
  After 24days, total activity of iodine-131 remaining in the patient body is estimated to be 400 Bq.
  Calculate the biological half life of iodine-131 in the body of the patient( ans : 18 days)
  
  Thx to those who can help.

• eagle

  1 Jun 08, 00:54

  1)The radioactive isotope 232,92U (meaning mass number =232, proton number = 92) emits alpha particles with an energy of 5.30MeV and has a half life of 74years. For a sample containing 1.30 X 10^24 atoms, calculate the maximum theoretical power output. ( ans : 3300W)

  Check the answer again... I got 330W

   

  Solution:
  
  Power = change in N * 5.3MeV / change in T (in seconds) = dN / dT * 5.3MeV

  The largest value of dN/dT occurs at N = 1.3e24 since

  

  so, subsitutiting N, and lambda = ln 2 / (74*365*24*3600s), and 1eV = 1.602e-19 W,

  answer to 2 sf is 330W

  the negative sign is removed since it shows N2 (final) - N1 (initial)

• eagle

  1 Jun 08, 01:01

  
  2)A patient is to be given an injection of iodine-131 in investigation of her blood volume.Sample A is injected into the patient while sample B is set on one side.
  Each sample has an initial activity of 8000 Bq and iodine-131 has halflife of 8 days.
  
  After 24days, total activity of iodine-131 remaining in the patient body is estimated to be 400 Bq.
  Calculate the biological half life of iodine-131 in the body of the patient( ans : 18 days)

   

  I think some values somewhere is wrong... I think maybe initial should be 1000Bq instead of 8000Bq... Recheck... Anyway... my solution:

   

  
  

  

  Let N0 = 8000
  N(t) = 400
  so exp(-λt) = 400/8000 = 1/20
  -λt = ln (1/20) = -2.99573, where t = 24 days

  so λ = 0.124822, where λ = ln 2 / half-life

  Thus, ln 2 / half-life = 0.124822
  half-life = 5.6 days